Uniform 10-polytope
10-simplex |
Truncated 10-simplex |
Rectified 10-simplex |
|||||||||
Cantellated 10-simplex |
Runcinated 10-simplex |
||||||||||
Stericated 10-simplex |
Pentallated 10-simplex |
Hexicated 10-simplex |
|||||||||
Heptellated 10-simplex |
Octellated 10-simplex |
Ennecated 10-simplex |
|||||||||
10-orthoplex |
Truncated 10-orthoplex |
Rectified 10-orthoplex |
|||||||||
10-cube |
Truncated 10-cube |
Rectified 10-cube |
|||||||||
10-demicube |
Truncated 10-demicube |
||||||||||
In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets.
A uniform 10-polytope is one which is vertex-transitive, and constructed from uniform facets.
A proposed name for 10-polytope is polyxennon (plural: polyxenna), created from poly- xenna (a variation on ennea meaning nine) and -on.
Contents |
Regular 10-polytopes
Regular 10-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v,w,x}, with x {p,q,r,s,t,u,v,w} 9-polytope facets around each peak.
There are exactly three such convex regular 10-polytopes:
- {3,3,3,3,3,3,3,3,3} - 10-simplex
- {4,3,3,3,3,3,3,3,3} - 10-cube
- {3,3,3,3,3,3,3,3,4} - 10-orthoplex
There are no nonconvex regular 10-polytopes.
Euler characteristic
The Euler characteristic for 10-polytopes that are topological 9-spheres (including all convex 10-polytopes) is zero. χ=V-E+F-C+f4-f5+f6-f7+f8-f9=0.
Uniform 10-polytopes by fundamental Coxeter groups
Uniform 10-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A10 | [39] | |
| 2 | B10 | [4,38] | |
| 3 | D10 | [37,1,1] | |
Selected regular and uniform 10-polytopes from each family include:
- Simplex family: A10 [39] -
- 527 uniform 10-polytopes as permutations of rings in the group diagram, including one regular:
- {39} - 10-simplex -
- 527 uniform 10-polytopes as permutations of rings in the group diagram, including one regular:
- Hypercube/orthoplex family: B10 [4,38] -
- 1023 uniform 10-polytopes as permutations of rings in the group diagram, including two regular ones:
- {4,38} - 10-cube or dekeract -
- {38,4} - 10-orthoplex or decacross -
- h{4,38} - 10-demicube .
- 1023 uniform 10-polytopes as permutations of rings in the group diagram, including two regular ones:
- Demihypercube D10 family: [37,1,1] -
- 767 uniform 10-polytopes as permutations of rings in the group diagram, including:
- 17,1 - 10-demicube or demidekeract -
- 71,1 - 10-orthoplex -
- 767 uniform 10-polytopes as permutations of rings in the group diagram, including:
The A10 family
The A10 family has symmetry of order 39,916,800 (11 factorial).
There are 512+16-1=527 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. 31 are shown below: all one and two ringed forms, and the final omnitruncated form. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 |
t0{3,3,3,3,3,3,3,3,3} |
11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | |
| 2 |
t1{3,3,3,3,3,3,3,3,3} |
495 | 55 | |||||||||
| 3 |
t2{3,3,3,3,3,3,3,3,3} |
1980 | 165 | |||||||||
| 4 |
t3{3,3,3,3,3,3,3,3,3} |
4620 | 330 | |||||||||
| 5 |
t4{3,3,3,3,3,3,3,3,3} |
6930 | 462 | |||||||||
| 6 |
t0,1{3,3,3,3,3,3,3,3,3} |
550 | 110 | |||||||||
| 7 |
t0,2{3,3,3,3,3,3,3,3,3} |
4455 | 495 | |||||||||
| 8 |
t1,2{3,3,3,3,3,3,3,3,3} |
2475 | 495 | |||||||||
| 9 |
t0,3{3,3,3,3,3,3,3,3,3} |
15840 | 1320 | |||||||||
| 10 |
t1,3{3,3,3,3,3,3,3,3,3} |
17820 | 1980 | |||||||||
| 11 |
t2,3{3,3,3,3,3,3,3,3,3} |
6600 | 1320 | |||||||||
| 12 |
t0,4{3,3,3,3,3,3,3,3,3} |
32340 | 2310 | |||||||||
| 13 |
t1,4{3,3,3,3,3,3,3,3,3} |
55440 | 4620 | |||||||||
| 14 |
t2,4{3,3,3,3,3,3,3,3,3} |
41580 | 4620 | |||||||||
| 15 |
t3,4{3,3,3,3,3,3,3,3,3} |
11550 | 2310 | |||||||||
| 16 |
t0,5{3,3,3,3,3,3,3,3,3} |
41580 | 2772 | |||||||||
| 17 |
t1,5{3,3,3,3,3,3,3,3,3} |
97020 | 6930 | |||||||||
| 18 |
t2,5{3,3,3,3,3,3,3,3,3} |
110880 | 9240 | |||||||||
| 19 |
t3,5{3,3,3,3,3,3,3,3,3} |
62370 | 6930 | |||||||||
| 20 |
t4,5{3,3,3,3,3,3,3,3,3} |
13860 | 2772 | |||||||||
| 21 |
t0,6{3,3,3,3,3,3,3,3,3} |
34650 | 2310 | |||||||||
| 22 |
t1,6{3,3,3,3,3,3,3,3,3} |
103950 | 6930 | |||||||||
| 23 |
t2,6{3,3,3,3,3,3,3,3,3} |
161700 | 11550 | |||||||||
| 24 |
t3,6{3,3,3,3,3,3,3,3,3} |
138600 | 11550 | |||||||||
| 25 |
t0,7{3,3,3,3,3,3,3,3,3} |
18480 | 1320 | |||||||||
| 26 |
t1,7{3,3,3,3,3,3,3,3,3} |
69300 | 4620 | |||||||||
| 27 |
t2,7{3,3,3,3,3,3,3,3,3} |
138600 | 9240 | |||||||||
| 28 |
t0,8{3,3,3,3,3,3,3,3,3} |
5940 | 495 | |||||||||
| 29 |
t1,8{3,3,3,3,3,3,3,3,3} |
27720 | 1980 | |||||||||
| 30 |
t0,9{3,3,3,3,3,3,3,3,3} |
990 | 110 | |||||||||
| 31 | t0,1,2,3,4,5,6,7,8,9{3,3,3,3,3,3,3,3,3} Omnitruncated 10-simplex |
199584000 | 39916800 | |||||||||
The B10 family
There are 1023 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings.
Twelve cases are shown below: ten single-ring (rectified) forms, and two truncations. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | t0{4,3,3,3,3,3,3,3,3} 10-cube (deker) |
20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | |
| 2 | t0,1{4,3,3,3,3,3,3,3,3} Truncated 10-cube (tade) |
51200 | 10240 | |||||||||
| 3 | t1{4,3,3,3,3,3,3,3,3} Rectified 10-cube (rade) |
46080 | 5120 | |||||||||
| 4 | t2{4,3,3,3,3,3,3,3,3} Birectified 10-cube (brade) |
184320 | 11520 | |||||||||
| 5 | t3{4,3,3,3,3,3,3,3,3} Trirectified 10-cube (trade) |
322560 | 15360 | |||||||||
| 6 | t4{4,3,3,3,3,3,3,3,3} Quadrirectified 10-cube (terade) |
322560 | 13440 | |||||||||
| 7 | t4{3,3,3,3,3,3,3,3,4} Quadrirectified 10-orthoplex (terake) |
201600 | 8064 | |||||||||
| 8 | t3{3,3,3,3,3,3,3,4} Trirectified 10-orthoplex (trake) |
80640 | 3360 | |||||||||
| 9 | t2{3,3,3,3,3,3,3,3,4} Birectified 10-orthoplex (brake) |
20160 | 960 | |||||||||
| 10 | t1{3,3,3,3,3,3,3,3,4} Rectified 10-orthoplex (rake) |
2880 | 180 | |||||||||
| 11 | t0,1{3,3,3,3,3,3,3,3,4} Truncated 10-orthoplex (take) |
3060 | 360 | |||||||||
| 12 | t0{3,3,3,3,3,3,3,3,4} 10-orthoplex (ka) |
1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | |
The D10 family
The D10 family has symmetry of order 1,857,945,600 (10 factorial x 29).
This family has 3×256−1=767 Wythoffian uniform polytopes, generated by marking one or more nodes of the D10 Coxeter-Dynkin diagram. Of these, 511 (2×256−1) are repeated from the B10 family and 256 are unique to this family, with 2 listed below. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | 10-demicube (hede) |
532 | 5300 | 24000 | 64800 | 115584 | 142464 | 122880 | 61440 | 11520 | 512 | |
| 2 | Truncated 10-demicube (thede) |
195840 | 23040 | |||||||||
Regular and uniform honeycombs
There are four fundamental affine Coxeter groups that generate regular and uniform tessellations in 9-space:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | 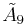 |
[3[10]] | |
| 2 | 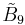 |
[4,37,4] | |
| 3 | 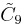 |
h[4,37,4] [4,36,31,1] |
|
| 4 | 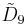 |
q[4,37,4] [31,1,35,31,1] |
|
Regular and uniform tessellations include:
- Regular 9-hypercubic honeycomb, with symbols {4,37,4},
- Uniform alternated 9-hypercubic honeycomb with symbols h{4,37,4},
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 10, groups that can generate honeycombs with all finite facets, and a finite vertex figure. However there are 3 noncompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 9-space as permutations of rings of the Coxeter diagrams.
 = [31,1,34,32,1]: = [31,1,34,32,1]: |
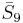 = [4,35,32,1]: = [4,35,32,1]: |
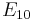 or or 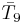 = [36,2,1]: = [36,2,1]: |
Three honeycombs from the 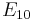 family, generated by end-ringed Coxeter diagrams are:
family, generated by end-ringed Coxeter diagrams are:
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Richard Klitzing, 10D, uniform polytopes (polyxenna)
External links
- Polytope names
- Polytopes of Various Dimensions, Jonathan Bowers
- Multi-dimensional Glossary
- Glossary for hyperspace, George Olshevsky.
| Family | An | BCn | Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular polygon | Triangle | Square | Hexagon | Pentagon | ||||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| n-polytopes | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||